3.2.11. responseSpectrumAnalysis Command

This command is used to perform a response spectrum analysis.
The response spectrum analysis performs N linear analysis steps, where N is the number of eigenvalues requested in a previous call to eigen Command.
For each analysis step, it computes the modal displacements. When the i-th analysis step is complete, all previously defined recorders will be called, so they will record all the results requested by the user, pertaining to the current modal displacements.
The modal combination of these modal displacements (and derived results such as beam forces) is up to the user, and can be easily done via TCL or Python scripting.

The command can be called in two different ways, depending on how you store the Tn/Sa (response spectrum function) values.

They can be either stored in a timeSeries …

responseSpectrumAnalysis $tsTag $direction <-scale $scale> <-mode $mode>

… or in two lists

responseSpectrumAnalysis $direction -Tn $Tn -Sa $Sa <-scale $scale> <-mode $mode>

Argument	Type	Description
$tsTag	integer	The tag of a previously defined Time Series Command. This list stores the Tn and Sa values. If you want to use the timeSeries, you cannot specify the -Tn and -Sa options
-Tn	string	Tells the command to use the $Tn list, instead of the timeSeries, to get the periods of the response spectrum function
$Tn	list float	The list of periods of the response spectrum function
-Sa	string	Tells the command to use the $Sa list, instead of the timeSeries, to get the accelerations of the response spectrum function
$Sa	list float	The list of accelerations of the response spectrum function
$direction	integer	The 1-based index of the excited DOF (1 to 3 for 2D problems, or 1 to 6 for 3D problems).
-scale	string	Tells the command to use a user-defined scale factor for the computed modal displacements. Not used, placeholder for future implementation.
$scale	float	User-defined scale factor for the computed modal displacements. Not used, placeholder for future implementation.
-mode	string	Tells the command to compute the modal displacements for just 1 specified mode (by default all modes are processed).
$mode	integer	The 1-based index of the unique mode to process.

Note

This command can be used only if a previous call to eigen Command and modalProperties Command has been performed.
It computes only the modal displacements, any modal combination is up to the user.
The scale factor (-scale $scale) for the output modal displacements is not used now, and it’s there for future implementations. When your model is linear elastic there is no need to use this option. It will be useful in future when we will allow using this command on a nonlinear model as a linear perturbation about a certain nonlinear state. In that case, the scale factor can be set to a very small number, so that the computed modal displacements will be very small (linear perturbation) and will not alter the nonlinear state of your model. Then the inverse of the scale factor can be used to post-multiply any result for post-processing.

3.2.11.1. Theory

Once the eigenvalue problem (eigen Command) has been solved, and once the modal properties (modalProperties Command) have been computed, the modal displacements $U$ for mode $i$ at node $n$ and DOF $j$ is given by

\[U_{ij}^n = \frac{\Phi_{ij}^n \cdot MPF_{ij} \cdot RSf\left(T_i\right)}{\lambda_i}\]

where:

$\lambda_i$ is the eigenvalue

$\Phi_{ij}^n$ is the eigenvector

$MPF_{ij}$ is the modal participation factor

$RSf\left(T_i\right)$ is the response spectrum function value at period $T_i$

and $T_i$ is the period $\frac{2\pi}{\sqrt{\lambda_i}}$

Example 1: Simple call

The following example shows how to call the responseSpectrumAnalysis command for all modes, using the time series 1 (or lists Tn and Sa) along the DOF 1 (Ux)

Tcl Code using timeSeries

set tsTag 1; # use the timeSeries 1 as response spectrum function
set direction 1; # excited DOF = Ux
responseSpectrumAnalysis $tsTag $direction

Tcl Code using lists

set Tn {0.0 0.1 0.4 .... }; # the periods
set Sa {1.9 3.7 4.9 .... }; # the accelerations
set direction 1; # excited DOF = Ux
responseSpectrumAnalysis $direction -Tn $Tn -Sa $Sa

Tcl Code using expanded lists

set Tn {0.0 0.1 0.4 .... }; # the periods
set Sa {1.9 3.7 4.9 .... }; # the accelerations
set direction 1; # excited DOF = Ux
responseSpectrumAnalysis $direction -Tn {*}$Tn -Sa {*}$Sa

Python Code using timeSeries

tsTag = 1 # use the timeSeries 1 as response spectrum function
direction = 1 # excited DOF = Ux
responseSpectrumAnalysis(tsTag, direction)

Python Code using lists

Tn = [0.0 0.1 0.4 .... ] # the periods
Sa = [1.9 3.7 4.9 .... ] # the accelerations
responseSpectrumAnalysis(direction, '-Tn', *Tn, '-Sa', *Sa)

Example 2: Iterative call

The following example shows how to call the responseSpectrumAnalysis command for 1 mode at a time, using the time series 1 along the DOF 1 (Ux)

Tcl Code

set tsTag 1; # use the timeSeries 1 as response spectrum function
set direction 1; # excited DOF = Ux
for {set i 0} {$i < $num_modes} {incr i} {
   responseSpectrumAnalysis $tsTag $direction -mode [expr $i+1]
   # grab your results here for the i-th modal displacements
}

Python Code

tsTag = 1 # use the timeSeries 1 as response spectrum function
direction = 1 # excited DOF = Ux
for i in range(num_modes):
   responseSpectrumAnalysis(tsTag, direction, '-mode', i+1)
   # grab your results here for the i-th modal displacements

Example 3: Complete Structural Example

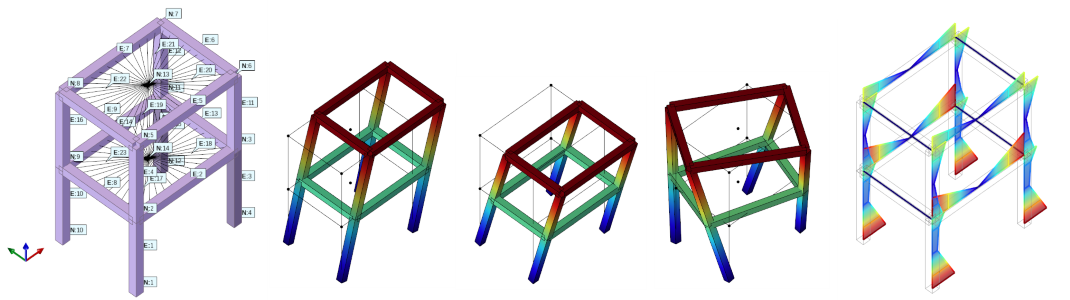
../../../_images/responseSpectrumAnalysis.png

The following example show a simple 1-bay 2-story building with rigid diaphragms. Units are Newton and meters.

It shows how to:

call the eigen Command to extract 7 modes of vibration

call the modalProperties Command to generate the report with modal properties

call the responseSpectrumAnalysis Command to compute the modal displacements and section forces * in a first example the responseSpectrumAnalysis Command is called for all modes. Results are obtained from a recorder after the analysis. * in a second example the responseSpectrumAnalysis Command is called in a for-loop mode-by-mode. Results are obtained within the for-loop usin the eleResponse

do a CQC modal combination

responseSpectrumAnalysisExample.tcl (TCL).

responseSpectrumAnalysisExample.py (Python).

Code Developed by: Massimo Petracca at ASDEA Software, Italy