Curved arch
April 2020, Amir Hossein Namadchi
This is an OpenSeesPy simulation of one of the numerical examples in A robust composite time integration scheme for snap-through problems by Yenny Chandra et. al. It’s a special problem involving dynamic snap-through with large deformations in elastic range. In their study, a new three sub-step composite time integration algorithm was presented to handle such problems. Here, I will use the Bathe scheme (TRBDF2) to perform transient analysis.

import numpy as np
from sees import render
import opensees.openseespy as ops
import matplotlib.pyplot as plt
from time import process_time
Below, the base units are defined as python variables:
# Units
mm = 1.0 # milimeters
N = 1.0 # Newtons
sec = 1.0 # Seconds
# Create the model
def arch_model(
Rise = 500,
Offset = 200,
L = None, #5000,
Angle = None,
Radius = None,
ne = 10):
# Define material parameters
E = 200
A = 1e4
I = 1e8
# Compute radius
if Radius is None:
Radius = Rise/2 + (2*L)**2/(8*Rise)
th = 2*(np.pi/2 - Angle)
else:
L = 0.5*np.sqrt(8*Rise*(Radius - Rise/2))
th = 2*np.arcsin(L/Radius)
#
# Build the model
#
model = ops.Model(ndm=2, ndf=3)
# Create nodes
nen = 2
nn = ne*(nen-1)+1
mid = (nn+1)//2 # midpoint node
for i, angle in enumerate(np.linspace(-th/2, th/2, nn)):
tag = i + 1
# Compute x and add offset if midpoint
x = Radius*np.sin(angle)
if tag == mid:
x -= Offset
# Compute y
y = Radius*np.cos(angle) - Radius*np.cos(-th/2)
# create the node
model.node(tag, x, y)
# Create elements
transfTag = 1
model.geomTransf("Corotational", transfTag)
for i in range(ne):
tag = i+1
nodes = (i+1, i+2)
model.element("ElasticBeamColumn", tag, *nodes, A, E, I, transfTag)
model.fix( 1, 1, 1, 0)
model.fix(nn, 1, 1, 0)
# Create a load pattern that scales linearly
model.pattern("Plain", 1, "Linear")
# Add a nodal load to the pattern
model.load(mid, 0.0, -1.0, 0.0, pattern=1)
model.system("ProfileSPD")
# model.system("FullGeneral")
# model.system("BandGeneral")
# model.system("Umfpack", det=True)
model.test("NormUnbalance", 1e-6, 25, 0)
model.algorithm("Newton")
model.analysis("Static")
return model, mid
arch_model(15.39553, 0, Angle=0.2014, Radius=762, ne=20)
Output:
(<opensees.openseespy.Model at 0x7f5666f598e0>, 11)
Model Defintion
# Node Coordinates Matrix (size : nn x 3)
node_coords = np.array([[-152.4, 0], [-137.337, 2.91714],
[-122.218, 5.53039], [-107.049, 7.8387],
[-91.8371, 9.84114], [-76.5878, 11.5369],
[-61.3076, 12.9252], [-46.0024, 14.0057],
[-30.6787, 14.7777], [-15.3424, 15.2411],
[0, 15.3955], [15.3424, 15.2411],
[30.6787, 14.7777], [46.0024, 14.0057],
[61.3076, 12.9252], [76.5878, 11.5369],
[91.8371, 9.84114], [107.049, 7.8387],
[122.218, 5.53039], [137.337, 2.91714],
[152.4, 0]], dtype = np.float64)*mm
# Element Connectivity Matrix (size: nel x 2)
connectivity = [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6],
[6, 7], [7, 8], [8, 9], [9, 10], [10, 11],
[11, 12], [12, 13], [13, 14], [14, 15],
[15, 16], [16, 17], [17, 18], [18, 19],
[19, 20], [20, 21]]
# Get Number of total Nodes
nn = len(node_coords)
# Get Number of total Elements
nel = len(connectivity)
#Boundary Conditions (size: fixed_nodes x 4)
B_C = [[1,1,1,1],
[nn,1,1,1]]
# Modulus of Elasticity
E = 206843*(N/mm**2)
# Mass Density
rho = (7.83e-9)*(N*(sec**2)/(mm**4))
# Cross-sectional area, 2nd Moment of Inertia
A = 12.7*0.6096*mm*mm
I = (1/12)*(12.7*(0.6096**3))*mm**4
model = ops.Model( ndm=2, ndf=3)
# Adding nodes to the model object using list comprehensions
for n in range(nn):
model.node(n+1,*node_coords[n])
# Applying BC
for n in range(len(B_C)):
model.fix(B_C[n][0],*B_C[n][1:])
# Define Transformation
model.geomTransf('Corotational', 1)
# Adding Elements
for e in range(nel):
model.element('elasticBeamColumn', e+1, *connectivity[e],
A, E, I, 1, '-mass', rho*A,'-cMass',1)
Loading
# load function (Applied @ top node)
F = lambda t: (t if t<=8 else 8)*N
# Dynamic Analysis Parameters
dt = 0.0001
time = 15
time_domain = np.arange(0,time,dt)
# Loading Definition
model.timeSeries('Path', 1 , dt=dt,
values=np.vectorize(F)(time_domain),
time=time_domain)
model.pattern('Plain', 1, 1)
model.load(11, *[0.0, -1.0, 0.0], pattern=1)
# Analysis
model.constraints('Transformation')
model.numberer('RCM')
model.system('ProfileSPD')
model.test('NormUnbalance', 1e-6, 100)
model.algorithm('Newton')
model.integrator('TRBDF2')
model.analysis('Transient')
# let's do this
time = [] # list to hold time stations for plotting
d_list = [] # list to hold vertical displacments of the top node
# start the timer
tic = process_time()
for i in range(len(time_domain)):
model.analyze(1, dt)
time.append(model.getTime())
d_list.append(model.nodeDisp(11,2))
# stop the timer
toc = process_time()
print('Time elapsed:',toc-tic, 'sec')
Output:
Time elapsed: 44.4480693 sec
Visualization
plt.figure(figsize=(14,5))
ax1 = plt.axes() # standard axes
plt.grid()
plt.yticks(fontsize = 14)
plt.xticks(fontsize = 14)
plt.title('Time history of vertical displacement of the top node',
{'fontstyle':'italic','size':18});
ax2 = plt.axes([0.65, 0.60, 0.2, 0.25])
ax1.plot(time, d_list,'k')
ax2.plot(time, d_list,'k')
ax2.set_xlim(left=13.5, right=14)
ax2.set_ylim(bottom=-15, top=-30)
ax1.set_xlabel('Time (sec)', {'fontstyle':'italic','size':14})
ax1.set_ylabel('Vertical Displacement (mm)', {'fontstyle':'italic','size':14});
Output:
<Figure size 1400x500 with 2 Axes>
Closure
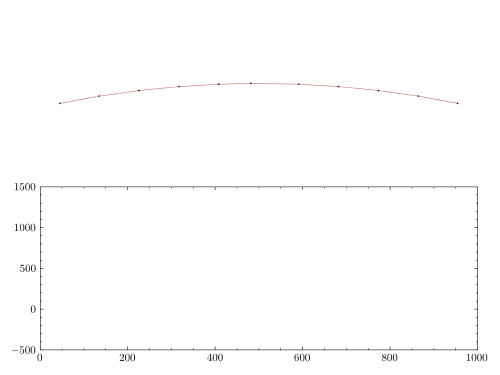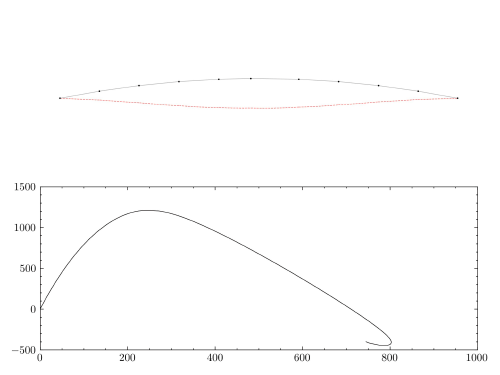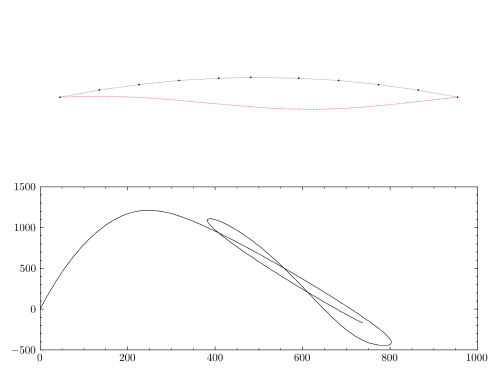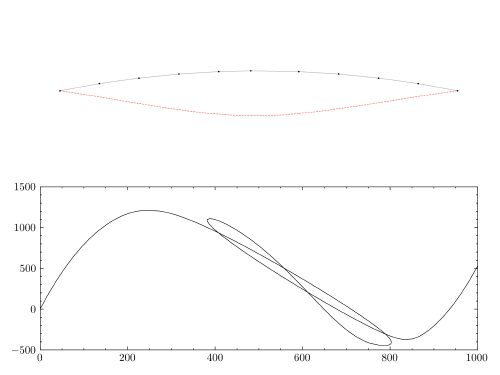
The figure deomnstrates a dynamic jump from the quasi static configuration. It then begins to oscillate around the remote equilibrium configuration. It is to be noted that conventional time integration algorithm like the Newmark method might not be able to present a stable and bounded solution like this. It is therefore necessary to employ an energy-conserving algorithms with proper numerical dissipation in order to tackle these kind of problems (like TRBDF2 and TRBDF3 in OpenSees).
References
-
Chandra, Y., Zhou, Y., Stanciulescu, I., Eason, T. and Spottswood, S., 2015. A robust composite time integration scheme for snap-through problems. Computational Mechanics, 55(5), pp.1041-1056.