3.1.10.19. ASDShellT3 Element

This command is used to construct an ASDShellT3 element object. The ASDShellT3 element is a 3-node general purpose thick shell element with the following features:

1. The membrane behavior is based on the ANDeS [Felippa2003] formulation, which uses the corner rotational DOFs (drilling DOFs) to improve the membrane behavior of the element.

2. The plate bending part is treated using the MITC3 [PSLee2004] formulation, to avoid the well known transverse shear locking behavior of thick plate elements.

3. Kinematics can be either linear or corotational. The corotational kinematics is based on the work of Felippa et al., i.e. the EICR [Felippa2000] [FelippaEtAl2005] (Element Independent Corotational formulation). Finite rotations are treated with Quaternions.

4. It uses 3 integration points to have a full rank for the ANDeS formulation and the MITC3 formulation. However, for computational efficiency, the user can optionally choose a single-point integration scheme. In this case, the 3 spurious zero-energy modes for the membrane behavior are constrained using the drilling DOF formulation according to Hughes-Brezzi [HughesEtAl1989] . This formulation constrains the drilling DOFs to the rigid body rotation via a penalty parameter as a function of the initial in-plane shear modulus. However, when using strain-softening materials, this (elastic) constraint may overstiffen the element as the in-plane shear modulus degrades. As a remedy in such a situation, the user can choose to make this constraint non-linear.

element ASDShellT3 $eleTag $n1 $n2 $n3 $secTag <-corotational> <-reducedIntegration> <-drillingNL> <-damp $dampTag> <-local $x1 $x2 $x3>

Argument	Type	Description
$eleTag	integer	unique integer tag identifying element object
$n1 $n2 $n3	3 integer	the three nodes defining the element (-ndm 3 -ndf 6)
$secTag	integer	unique integer tag associated with previously-defined SectionForceDeformation object
-corotational	string	optional flag, if provided, the element uses non-linear kinematics, suitable for large displacement/rotation problems.
-reducedIntegration	string	optional flag, if provided, the element uses 1-point integration rule.
-drillingNL	string	optional flag, if provided, the Hughes-Brezzi drilling DOF formulation considers the non-linear behavior of the section. Used only when -reducedIntegration is used.
-damp $dampTag	string + integer	optional, to activate elemental damping as per elementalDamping
-local $x1 $x2 $x3	string + 3 float	optional, if provided it will be used as the local-x axis of the element (otherwise the default local X will be the direction of the 1-2 side). Note: it will be automatically normalized and projected onto the element plane. It must not be zero or parallel to the shell’s normal vector.

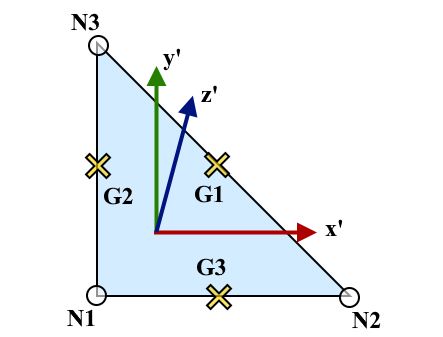
Fig. 3.1.10.20 Nodes, Gauss points and local coordinate system

Note

Valid queries to the ASDShellT3 element when creating an ElementRecorder object are:

• ‘force’, ‘forces’, ‘globalForce’, or ‘globalForces’:

  • Internal forces at the element’s nodes.

  • Orientation: global coordinate system.

  • Size: 18 columns of data, 6 components for each one of the 3 nodes.

• ‘material $secTag $secArg1 … $secArgN’:

  • Section response at section $secTag

  • $secTag is the 1-based index of the integration point (1 to 3).

  • ‘$secArg1 … $secArgN’ are the arguments required by the SectionDeformationObject at the requested integration point.

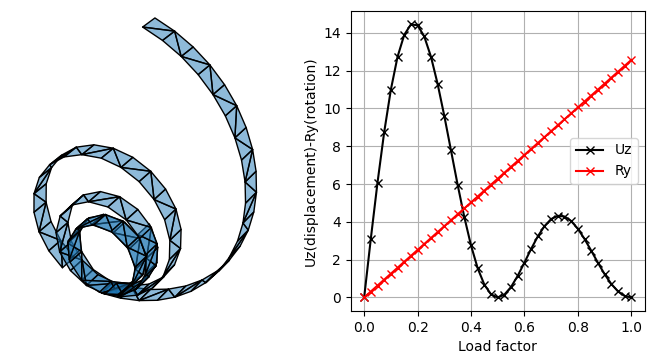
Example 1 - Cantilever Bending Roll-up (corotational)

A Cantilever beam is subjected to a total end-moment about the Y axis \(M_y = n 2 \pi EI/L\), where \(n\) is the number of rotations (2 in this example).

figures/ASDShellT3/ASDShellT3_Example_GNL_BendingRollUp.py

Code Developed by: Massimo Petracca at ASDEA Software, Italy.

[Felippa2003]

Felippa, Carlos A. “A study of optimal membrane triangles with drilling freedoms.” Computer Methods in Applied Mechanics and Engineering 192.16-18 (2003): 2125-2168. (Link to article)

[PSLee2004]

Lee, Phill-Seung, and Klaus-Jürgen Bathe. “Development of MITC isotropic triangular shell finite elements.” Computers & Structures 82.11-12 (2004): 945-962. (Link to article)

[Felippa2000]

Felippa, Carlos A. “A systematic approach to the element-independent corotational dynamics of finite elements”. Technical Report CU-CAS-00-03, Center for Aerospace Structures, 2000. (Link to article)

[FelippaEtAl2005]

Felippa, Carlos A., and Bjorn Haugen. “A unified formulation of small-strain corotational finite elements: I. Theory.” Computer Methods in Applied Mechanics and Engineering 194.21-24 (2005): 2285-2335. (Link to article)

[HughesEtAl1989]

Hughes, Thomas JR, and F. Brezzi. “On drilling degrees of freedom.” Computer methods in applied mechanics and engineering 72.1 (1989): 105-121. (Link to article)