3.1.6.10. DuctileFracture Material

This command is used to construct a uniaxial material object for simulating reinforcement steel fracture under monotonic/cyclic loads. The material is based on a newly developed Reinforcement Ductile Fracture Model (RDFM) ([Zhong2021], [ZhongDeierlein2022a]).

uniaxialMaterial DuctileFracture $matTag $baseTag -c_momo $c_mono -c_cycl $c_cycl -c_symm $c_symm <-E_s $E_s> <-esu $esu> <-k1 $k1> <-k2 $k2> <-db $db> <-b1 $b1> <-b2 $b2> <-FImax $FImax>

Argument	Type	Description
$matTag	integer	integer tag identifying material
$baseTag	integer	integer tag identifying the base material (describing the constitutive model) wrapped by DuctileFracture
$c_mono	float	void-growth coefficient
$c_cycl	float	cyclic deterioration coefficient
$c_symm	float	symmetry coefficient
$E_s	float	initial elastic tangent (optional: default = 29000.0 ksi).
$esu	float	uniform strain of the reinforcement
$k1	float	Necking Amplification Model strain coefficient (optional: default = 1.0). see note.
$k2	float	Necking Amplification Model stress coefficient (optional: default = 0.0). see note.
$db	float	bar diameter (optional: only used when considering bar buckling). see note.
$b1	float	Buckling Adjustment Model amplitude coefficient (optional: default = 0.0). see note.
$b2	float	Buckling Adjustment Model strain coefficient (optional: default = 1000.0). see note.
$FImax	float	Fracture Index at bar fracture (optional: default = 1.0).

Note

The RDFM extends the previous studies on simulating ductile fractures of structural steel materials (e.g., [KavindeDeierlein2007], [SmithEtAl2017]) to quantify the damage of reinforcing steel material by a Fracture Index ($FI$):

\[FI = Ce^{\lambda \int_{T<0} d\epsilon_p}\int(\beta e^{1.3T}-e^{-1.3T})d\epsilon_p\]

where modeling parameters are $C$ (void-growth coefficient), $\lambda$, and $\beta$ in the FI equation. $T$ is stress triaxiaility, the ratio of hydrostatic stress and effective stress. $\lambda$ and $\beta$ are path-dependent:

\[ \begin{align}\begin{aligned}\beta = 1.0+(\beta_0-1.0)\left[\frac{min(\Delta\epsilon_{max},\Delta\epsilon_{th})}{\Delta\epsilon_{th}}\right]^\gamma\\\lambda = \lambda_0\left[\frac{min(\Delta\epsilon_{max},\Delta\epsilon_{th})}{\Delta\epsilon_{th}}\right]^\gamma\end{aligned}\end{align} \]

where $\lambda_0$ is cyclic deterioration coefficient, and $\beta_0$ is symmetry coefficient. These three coefficients $C$, $\lambda_0$, and $\beta_0$ are material specific which corresponds to different fracture resistances for different reinforcing steel materials. Given a plastic steel strain history, the influence of these three coefficients on $FI$ are show in Fig. 3.1.6.7. In DuctileFracture, $C$, $\lambda_0$, and $\beta_0$ are $c_mono, $c_cycl, and $c_symm, respectively.

Comparing to traditional Coffin-Manson fatigue model, the RDFM can (1) predict ultra-low cycle and monontonic bar fracture based on void growth/shrinkage mechanism, (2) simulate the influence of buckling-induced strain localization on bar fracture, and (3) consider the path-dependency of buckling effects on longitudinal bar ruptures in reinforced concrete beams and columns. These features are implemented as the Necking Amplification Model (NAM) and Buckling Adjustment Model (BAM) as shown in the flowchart Fig. 3.1.6.8.

The two NAM modeling coefficients $k_1$ ($k1) and $k_2$ ($k2) are calibrated to reinforcing steel bar fracture test data, and the two BAM modeling coefficients $b1$ ($b_1) and $b2$ ($b2) are calibrated to cyclic bar fatigue test data with observed buckling effects. Based on the calibration, along with $C$, $\lambda_0$, and $\beta_0$, the modeling coefficients in the DuctileFracture are suggested to be estimated by ([Zhong2021], [ZhongDeierlein2022b]):

\[ \begin{align}\begin{aligned}C = e^{-3.96-1.85ln\epsilon_{su}+0.20ln\left(\frac{d_b}{8in}\right)}\\\lambda_0 = e^{5.90+1.53ln\left(\frac{f_y}{60ksi}\right)+2.32ln\epsilon_{su}+1.11ln\left(\frac{d_b}{8in}\right)}\\\beta_0 = 1.05\\k_1 = e^{2.21-0.32ln\left(\frac{T}{Y}\right)-0.66ln\left(\frac{d_b}{8in}\right)}\\k_2 = e^{1.29+0.64ln\left(\frac{f_y}{60ksi}\right)-0.46ln\left(\frac{d_b}{8in}\right)}\\b_1 = e^{-2.53-1.90ln\left(\frac{T}{Y}\right)-1.36ln\left(\frac{d_b}{8in}\right)-0.43ln\left(\frac{R_{min}}{1.5H}\right)}\\b_2 = e^{-3.29-0.49ln\epsilon_{su}-0.14ln\left(\frac{R_{min}}{1.5H}\right)-0.70ln\left(\frac{s^*}{d_b}\right)}\end{aligned}\end{align} \]

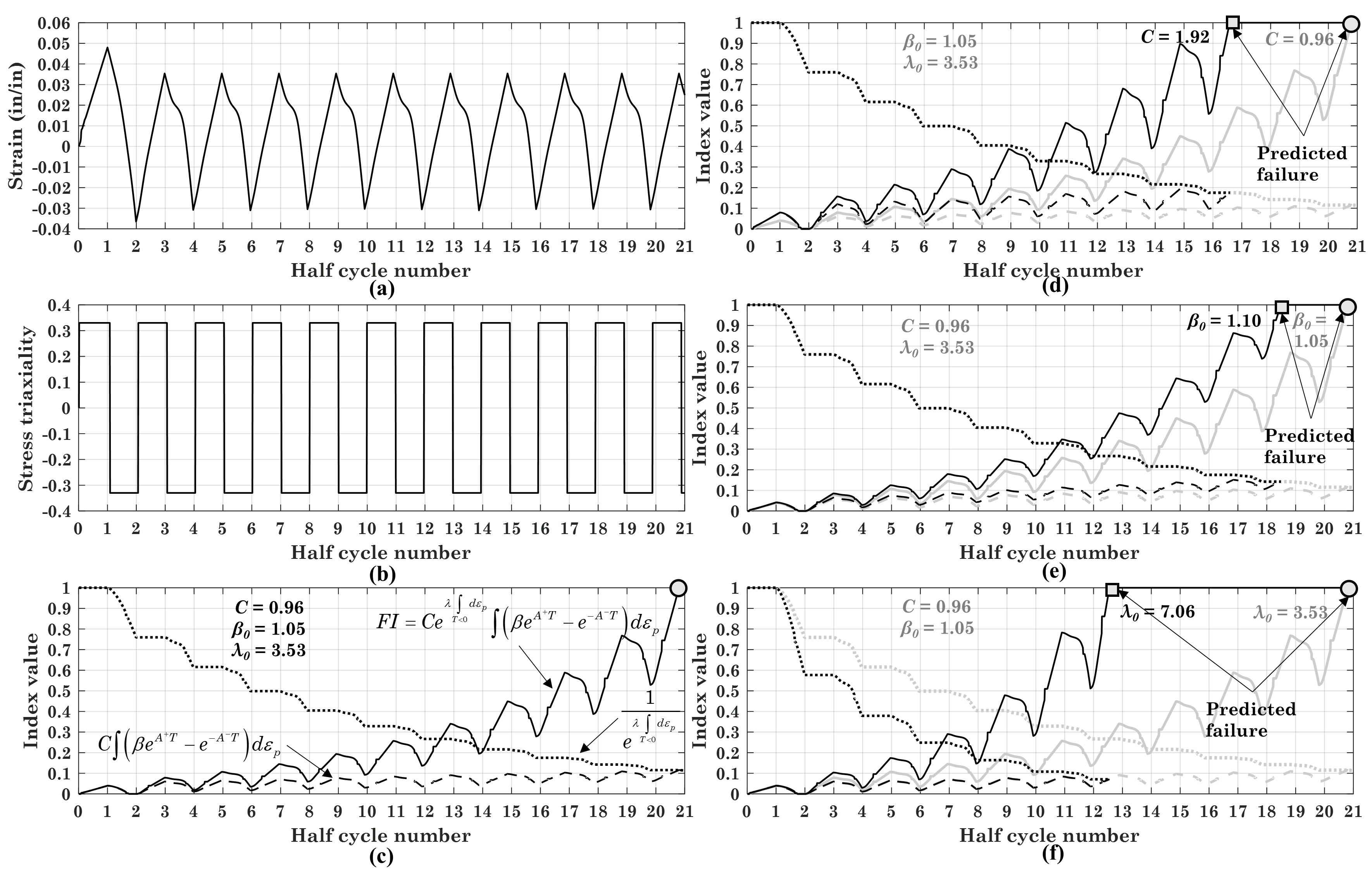
../../../../_images/DuctileFracture_mp_infl.png — Fig. 3.1.6.7 Influence of $C$, $\lambda_0$, and $\beta_0$ on $FI$.

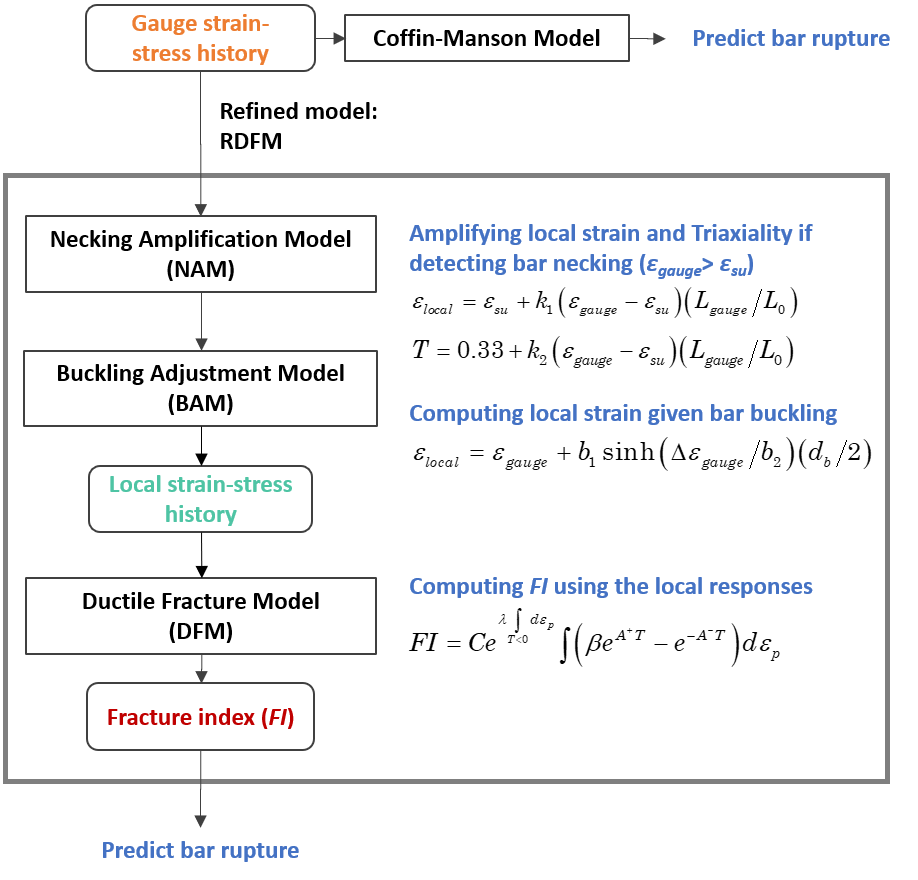
../../../../_images/DuctileFracture_Workflow.png — Fig. 3.1.6.8 Reinforcement Ductile Fracture Simulation.

Example

The following is used to construct a DuctileFracture along with a base material using ReinforcingSteel.

Tcl Code

uniaxialMaterial Steel02 1 64.7 30944.0 0.012 18 0.925 0.15
uniaxialMaterial DuctileFracture 2 1 -c_mono 1.255 -c_cycl 1.383 -c_symm 1.05 -E_s 30944.0 -esu 0.10 -k1 11.30 -k2 4.49 -db 0.63 -b1 0.04 -b2 0.02;

[Zhong2021] (1,2)

Zhong, K. (2020). “Influence of Reinforcing Steel Fracture on Seismic Performance of Concrete Structures: Fracture Simulation, Earthquake Duration Effects, and Design Strategies”. PhD Dissertation, Stanford University.

[ZhongDeierlein2022a]

Zhong, K., Deierlein. G. G. (2022). “Reinforcement Fracture Simulation. I: Damage Model for Bare Bar Fatigue and Fracture”.

[ZhongDeierlein2022b]

Zhong, K., Deierlein. G. G. (2022). “Reinforcement Fracture Simulation. II: Predictive Equations and Application for Reinforcement in Concrete Structures”.

[KavindeDeierlein2007]

Kanvinde A M, Deierlein G G. (2007). “Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue”[J]. Journal of engineering mechanics, 133(6): 701-712.

[SmithEtAl2017]

Smith C, Kanvinde A, Deierlein G. (2017). “A local criterion for ductile fracture under low-triaxiality axisymmetric stress states”[J]. Engineering Fracture Mechanics, 169: 321-335.

Code Developed by: Kuanshi Zhong (kuanshi@stanford.edu), Gregory Deierlein