3.1.6.28. Hertz Damp Material

This command is used to construct the uniaxial Hertz Damp Material

uniaxialMaterial Hertzdamp $matTag $Kh $xiNorm $gap <$n>

Argument	Type	Description
$matTag	integer	integer tag identifying material.
$Kh	float	nonlinear Hertz contact stiffness.
$xiNorm	float	normalized impact damping ratio.
$gap	float	initial gap.
$n	float	indentation exponent (optional with default value of: 1.5).

Note

This material is implemented as a compression-only gap material, so $gap should be input as a negative value.

This material model follows the constitutive law

\[f_c (t) = k_h (\delta(t) -g)^n + c_h \dot{\delta}(t)\]

where t is time, $f_c (t)$ is the contact force, $k_h$ is the nonlinear Hertz contact stiffness ($Kh), $\delta(t)$ is the indentation, g is the initial gap ($gap), n is the indentation exponent ($n), and $\dot{\delta}(t)$ is the indentation velocity. The damping coefficient $c_h$ is computed as

\[c_h = \overline{\xi} \frac{k_h}{\dot{\delta}_0} (\delta(t) - g)^n\]

where $\dot{\delta}_0$ is the pre-impact indentation velocity. The normalized impact damping ratio $\overline{\xi}$ ($xiNorm) is usually related to the coefficient of restitution, represented by e. The recommended form of $\overline{\xi}$ is

\[\overline{\xi} = \frac{8}{5} \frac{1-e}{e}\]

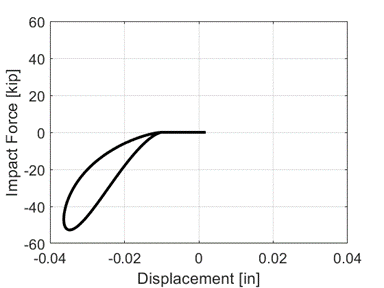
Response of the Hertzdamp material during impact:

Note that the flat displacement from 0 to roughly minus 0.01 inch displacement is caused by the gap parameter.

Code Developed by: Patrick J. Hughes, UC San Diego

[Lankarani1990]

Lankarani HM, Nikravesh PE. A Contact Force Model with Hysteresis Damping for Impact Analysis of Multibody Systems. Journal of Mechanical Design 1990; 112(3): 369–376. DOI: 10.1115/1.2912617.

[Muthukumar2006]

A Hertz contact model with non-linear damping for pounding simulation. Earthquake Engineering and Structural Dynamics 2006; 35(7): 811–828. DOI: 10.1002/eqe.557.

[YeK2009]

Ye K, Li L, Zhu H. A note on the Hertz contact model with nonlinear damping for pounding simulation. Earthquake Engineering and Structural Dynamics 2009; 38: 1135–1142. DOI: 10.1002/eqe.

[Hughes2020]

Evaluation of uniaxial contact models for moat wall pounding simulations. Earthquake Engineering and Structural Dynamics 2020(March): 12–14. DOI: 10.1002/eqe.3285.